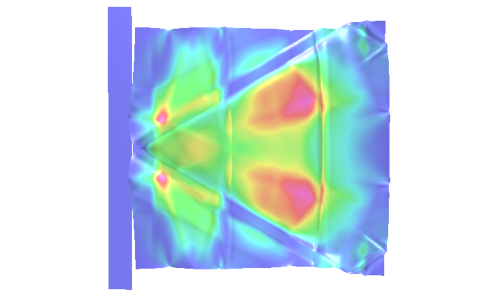
Our research interests are in general areas of applied mathematics, computational mechanics, computational electromagnetics and fracture modeling. The development of advanced numerical schemes, such as spacetime discontinuous Galerkin finite element methods, and the investigation of their convergence, efficiency, scalability, and robustness are some themes of our research. These methods are capable of obtaining extraordinarily efficient and accurate solutions for a wide array of multiphysics applications in solid, fluid, and thermal mechanics, electromagnetics, and acoustics, particularly for highly multiscale and parallel simulations and problems with nonsmooth features such as shocks and singular features.

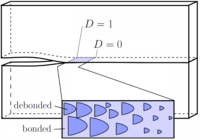
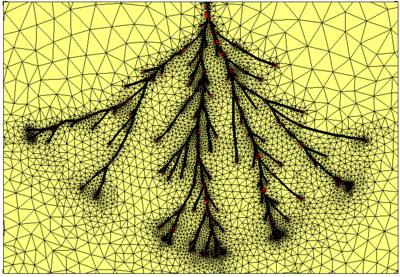
In addition, we combine theoretical, phenomenological, and computational approaches to derive new contact/fracture models. Some areas of research include dimensional analysis and comparison of various fracture models, dynamically consistent integrated contact/damage models, probabilistic crack propagation approach, and the development of a multiscale interfacial and bulk damage models through linking mesoscopic damage features to macroscopic crack surfaces and continuum constitutive models.